Is Money Continuous Or Discrete? Money can be both, depending on the context. Physical currency is discrete, while digital representations of money can behave more like continuous data, as explored further on money-central.com, offering solutions for personal finance management, savings, and investments.
1. Understanding Discrete Data
Discrete data involves countable, distinct values that exist only in set increments. These values are not divisible and are always separate. Discrete variables are limited in the number of possible values between two intervals, meaning there’s a finite number of “points” between points. A key characteristic is that it is countable, not measurable.
Discrete data does not always have to be numbers. It can include ordinal data, like sliding scales, or letter grading systems. One downside is its limited granularity, where users can only subdivide variables into their smallest units, limiting precision. However, this can allow users to work with integers more quickly and easily.
1.1 Examples of Discrete Variables
Discrete data describes physical or material entities, such as the number of students in a classroom or the inventory of computers in a store. It doesn’t make sense to have “17.5 devices.” Common examples include:
- Number of employees in a company
- Number of questions on a test
- Number of cars in a parking lot
- Number of pages in a book
- Number of rooms in a house
- Number of goals scored
- Number of tickets sold
 Close-up of a stack of tickets, symbolizing countable, distinct units of discrete data.
Close-up of a stack of tickets, symbolizing countable, distinct units of discrete data.
2. Understanding Continuous Data
Continuous data involves measurable information using infinitely divisible increments. Continuous variables have infinite possible intervals between values. For example, between 5 and 10, there are infinite decimals (7, 8.3, 6.825, 9.99999).
Continuous data allows for greater granularity and specificity, depending on the measurement tool. Physical measurements like weight are limited by the tool’s precision, while digital analytics can specify values to hundredths of a percent.
2.1 Examples of Continuous Variables
Continuous variables encompass data measured via an external scale, such as weight, height, and time. In a business context, continuous data includes product dimensions, average order value, and time spent on a project. Abstract measurements, like productivity or efficiency, are also continuous. Common examples include:
- Height or length of an object
- Age of a person
- Weight of an item
- Temperature outside
- Duration of a task
- Speed of a vehicle
- Blood pressure
- Heart rate
- GPA
- Sound intensity
- Brightness of a light
3. Discrete vs. Continuous: Identifying the Difference
Continuous data allows for more granularity, while discrete data is limited to a preset level of specificity. Discrete variables may be preferred for quick, high-level access to data.
To identify whether data is discrete or continuous, consider whether it can be calculated to greater precision depending on the tool or method. Measuring the number of people in a room (discrete) can never get more precise than the counted integer. Another way to think about it is whether there are infinite values within a given range.
3.1 Key Characteristics
| Discrete Data | Continuous Data |
|---|---|
| Countable | Not countable (infinite) |
| Cannot be divided beyond its base unit | Subdivisible |
| Less granularity | More granularity |
| Includes integer and ordinal values | Includes quantitative data (fractions, percentages, decimals) |
4. The Importance of Continuous and Discrete Data
Continuous data is often the default for business use due to its precision, but both types play key roles. Counts of inventory or the number of people on a project should be tracked as their discrete values. If businesses use discrete data to create continuous values, they still maintain the original discrete values. Using the different types properly is critical for effective analysis. For example, understanding what data assets are continuous and can be used in forecasting can make or break the reliability of that estimation.
Tracking various discrete variables like the number of projects completed, leads generated, or defective items not only helps to monitor performance over time, but also serves as the foundation of continuous calculations like averages, speeds, and more. Money-central.com can guide you through these data types for financial planning.
5. Graphical Representations and Visualizations
Because of their differences, discrete and continuous data are often represented with different methods and visualizations.
| Discrete Data | Continuous Data |
|---|---|
| Bar charts | Line charts |
| Pie charts | Density plots |
| Frequency tables | Area charts |
6. More Examples: Discrete vs. Continuous
Many categories of measurements will have both continuous and discrete metrics.
| Data Category | Discrete Variable Example | Continuous Variable Example |
|---|---|---|
| Product Sales | Number of units sold | Revenue from sales |
| Website Engagement | Number of site visits | Average time per session |
| Rainfall | Number of rainy days | Total rainfall amount |
| School Course Impact | Number of students enrolled | Average test scores |
| Investment Portfolio | Number of shares owned | Total value of portfolio |
7. How Businesses Use Continuous and Discrete Data
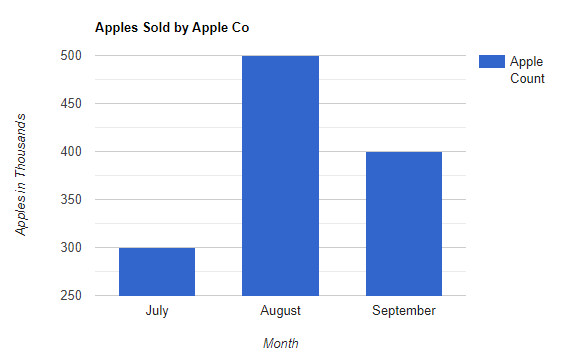
Businesses use both data types to make informed decisions. Discrete data helps in assessing quantities and counts, while continuous data provides precision for detailed analysis. Let’s explore how an imaginary apple company might use both types of data. Using discrete information, we can assess:
- Apples sold in the month of August
- Units of fuel used in transport
- Dollars of profit and expenses in August
- Number of trucks that broke down
These data points are essential for keeping a company flowing, are easily visualized in formats like bar charts, and are great for quick information. These data points are discrete because the company does not sell half apples.
However, the aggressive pace of efficiency and optimization makes the specificity of continuous variables a must for businesses. In our apple company, continuous data will show things like average sales per day, the weight of each shipment, and the rate of truck breakdowns. All of this precise and divisible data enables us to examine attributes such as spoilage rates and trend lines.
7.1 Apple Company Example: Discrete vs. Continuous
To demonstrate why this is so useful, here is an example of similar information, portrayed using continuous data versus discrete. If you are in charge of product quality and reported 10,000 spoiled apples in July and 12,000 in August, you have presented a rise in spoilage.
However, with continuous data, you could report that apple spoilage rate is actually down from 3.3% to 2.4%. This vast oversimplification shows the relative utility of both in a professional setting.
7.2 Turning Discrete into Continuous
Modern business processes will often convert discrete data to continuous data during analysis. Methods like regression analysis are common examples of this phenomenon. Take Net Promoter Scores (NPS) for example. This data point measures how likely users are to recommend a product on a discrete scale of whole numbers from 1-10.
A pool of discrete ratings on its own isn’t very helpful. Instead, a data analyst averages all NPS ratings to get an average NPS score. Depending on the averaged discrete values, the average NPS score could be specified as a continuous value, such as 7.483.
This granularity is crucial to tracking changes in the NPS score over time. Continuous NPS data can capture even small trends in the score over time. The business can also keep the original discrete values for data integrity. Today, most businesses use a range of statistical analysis software to surface business insights, incorporating both continuous and discrete data inputs.
8. Money as Discrete vs. Continuous: A Detailed Exploration
To truly grasp the nature of money, especially in financial analysis, it’s vital to understand whether it’s best considered as discrete or continuous. This distinction has profound implications for how we manage, analyze, and make decisions about our finances.
8.1. Physical Currency: The Discrete Nature of Cash
Physical money, like coins and banknotes, represents the quintessential example of discrete data. Each coin or bill has a fixed, indivisible value. In the U.S., you can have a penny ($.01), a nickel ($.05), a dime ($.10), a quarter ($.25), and so on. You cannot have a fraction of a cent in physical currency. This is because the value is countable and distinct.
Think about it: you can count the number of dollar bills in your wallet or the number of coins in your piggy bank. Each unit is separate and whole. According to research from the Federal Reserve, there are approximately 50.7 billion banknotes in circulation as of 2023. This vast but finite number underscores the discrete nature of physical currency.
The discrete nature of physical money has several implications:
- Transactions have a minimum increment: You can’t use physical currency to pay for something in an amount more precise than a cent. If something costs $12.345, you can only pay $12.34 or $12.35.
- Limited granularity: The level of detail you can achieve with physical money is limited to the available denominations.
- Simplicity: Discrete units are easy to understand and count, making physical money straightforward for everyday transactions.
8.2 Digital Money: Approaching Continuity
Digital money, represented by bank account balances, credit card transactions, and other electronic forms, introduces a different perspective. While still based on discrete units (cents), digital money behaves more like continuous data due to the high degree of divisibility and precision it allows.
Consider your bank account: you can have balances that include fractions of a cent, even though you can’t withdraw that fraction as physical currency. For instance, interest calculations or investment returns can result in balances like $1,234.5678. Although the smallest unit that can be transacted is still one cent, the accounting and record-keeping can operate at a much finer level of granularity.
The continuous-like nature of digital money has several advantages:
- Higher precision: Digital transactions allow for much more precise calculations and payments. Online retailers, for example, can charge exactly $19.99 for a product, and your credit card can handle the transaction without rounding.
- Complex financial instruments: Many sophisticated financial instruments, such as bonds, stocks, and derivatives, rely on the ability to track values with high precision. This is only possible with digital money.
- Algorithmic trading: High-frequency trading algorithms can make decisions based on minute price changes, which requires the continuous-like nature of digital currency.
8.3 The Hybrid Reality
In practice, money often exists in a hybrid state, combining aspects of both discrete and continuous data. You might use a credit card (digital money) to buy a cup of coffee (physical product) for $2.75. The transaction involves a continuous-like representation of money but ultimately settles as a discrete value.
Another example is your mortgage. While your monthly payment is a discrete amount, the interest is calculated based on a continuous-like interest rate applied to the outstanding balance, which can be tracked to fractions of a cent.
8.4 Implications for Financial Analysis
Understanding whether money is discrete or continuous (or a combination of both) is crucial for financial analysis. It affects how you model, forecast, and make decisions about money.
- Budgeting: When creating a budget, you typically deal with discrete amounts. You allocate a fixed number of dollars to various categories (rent, food, entertainment). However, when tracking expenses, you might encounter transactions that involve continuous-like precision (e.g., gas prices calculated to the tenth of a cent per gallon).
- Investment Analysis: Investment returns are often calculated with high precision, treating money as continuous. However, when you buy or sell stocks, you deal with discrete units (shares) at a specific price per share.
- Financial Modeling: In financial modeling, it’s common to treat money as continuous for calculations like compound interest or discounted cash flow analysis. However, you need to be mindful of the discrete nature of certain inputs, such as the number of years to project or the number of employees.
- Risk Management: Financial risk models often use continuous distributions to simulate potential losses or gains. However, regulatory requirements might impose discrete thresholds or capital requirements.
8.5 Real-World Examples
To illustrate these concepts, let’s consider a few real-world examples:
- Savings Account: Your savings account balance is tracked with continuous-like precision, allowing you to earn interest calculated to fractions of a cent. However, when you withdraw money, you can only withdraw whole cents.
- Credit Card Rewards: Credit card rewards are often calculated as a percentage of your spending. This results in rewards that are tracked to fractions of a cent, even though you can only redeem them in whole-cent increments.
- Mortgage Interest: Mortgage interest is calculated daily based on the outstanding balance, often using continuous-like interest rates. However, your monthly payment is a discrete amount.
- Stock Dividends: Stock dividends are declared as a certain amount per share. While the dividend per share is often expressed with high precision (e.g., $0.5678 per share), you receive a discrete amount based on the number of shares you own.
8.6 Case Studies
Let’s delve into specific case studies to illustrate how the discrete vs. continuous nature of money impacts financial decisions and outcomes.
Case Study 1: The Impact of Rounding Errors in High-Frequency Trading
- Background: High-frequency trading (HFT) firms use powerful computers and algorithms to execute a large number of orders at very high speeds. These algorithms often exploit tiny price discrepancies that may only exist for fractions of a second.
- Challenge: The discrete nature of order sizes (number of shares) and the continuous-like nature of stock prices create a challenge. When an HFT algorithm attempts to buy or sell a large number of shares, rounding errors can accumulate. Even small rounding errors can have a significant impact on profitability due to the high volume of trades.
- Solution: HFT firms use sophisticated techniques to minimize rounding errors. This includes optimizing order sizes, using specialized software that can handle fractional shares (in some markets), and continuously monitoring the impact of rounding on their overall performance. According to a study by the New York University’s Stern School of Business, effective management of rounding errors can improve HFT profitability by as much as 5-10%.
- Impact: By carefully managing rounding errors, HFT firms can maintain a competitive edge in the fast-paced world of high-frequency trading.
Case Study 2: The Role of Precision in Calculating Compound Interest
- Background: Compound interest is a powerful tool for wealth accumulation. The more frequently interest is compounded, the faster your money grows.
- Challenge: When calculating compound interest, the continuous-like nature of interest rates and the precision with which interest is calculated can have a significant impact on the final balance. The more precise the calculations, the more accurate the final result.
- Solution: Banks and financial institutions use sophisticated software to calculate compound interest with high precision. This ensures that customers receive the correct amount of interest and that the bank’s financial statements are accurate. A study by Forbes found that even small differences in interest calculation methods can result in significant variations in long-term returns.
- Impact: Accurate calculation of compound interest is essential for both consumers and financial institutions. It ensures that individuals can achieve their financial goals and that banks can maintain trust with their customers.
Case Study 3: The Challenges of Budgeting with Irregular Income
- Background: Many people have irregular income, such as freelancers, contractors, and small business owners. This makes budgeting more challenging.
- Challenge: Irregular income streams often require individuals to switch between treating money as a continuous flow for long-term planning and recognizing its discrete amounts when cash flow is restricted. Unlike those with fixed salaries, those with irregular income have to adapt constantly, allocating funds according to when the money arrives.
- Solution: Individuals with irregular income can use budgeting apps and software to track their income and expenses with high precision. This allows them to identify trends, set financial goals, and make informed decisions about their spending. Many apps also allow users to categorize expenses and set limits for each category, promoting better control.
- Impact: Effective budgeting can help people with irregular income achieve their financial goals and avoid debt. This is particularly important for those who are self-employed or own small businesses.
In summary, the discrete vs. continuous nature of money is a complex issue with significant implications for financial analysis. By understanding the nuances of how money behaves, you can make more informed decisions and improve your financial outcomes.
9. Discrete vs. Continuous FAQs
9.1 How can you tell if a graph is discrete or continuous?
Discrete graphs often have distinct parts (bars, points, etc.), while continuous graphs are typically represented with unbroken lines or areas (time series charts or area charts). To determine whether data can only be integers or could be further broken down into decimals, fractions, etc, it’s best to look at the dependent variable (usually along the vertical axis).
9.2 Is age discrete or continuous?
Age is a continuous variable because it can always be broken down further into more precise measurements (months, days, seconds, etc.). Any measurement of time, whether age, duration, or another derived metric (like miles per hour) is a continuous variable rather than discrete.
9.3 Is weight continuous or discrete?
Weight is also continuous because it can be measured at 150 lbs, 150.1 lbs, 150.13 lbs, and so on. However, if a dataset of weight is categorized into buckets (such as “Less than 50 lbs,” “Between 51 and 100 lbs,” etc.), that would be classified as discrete data because there are a finite number of assigned values.
9.4 Is money discrete or continuous?
This depends on the type of money — physical money like bills and coins are discrete because they can’t be used to pay amounts more specific than cents. In other words, you can’t use physical money to pay $12.3456. However, digital currency like credit cards and bank transfers may be classified as continuous because they could theoretically be subdivided more than physical money.
9.5 Can discrete data be converted into continuous data?
Yes, discrete data can be converted into continuous data through methods like averaging or regression analysis. For example, Net Promoter Scores (NPS), which are discrete ratings, can be averaged to create a continuous NPS score.
9.6 Why is it important to understand whether data is discrete or continuous?
Understanding whether data is discrete or continuous is crucial for effective analysis and decision-making. It affects how you model, forecast, and interpret data, as well as the types of visualizations and statistical methods you can use.
9.7 How do businesses use discrete and continuous data together?
Businesses use both discrete and continuous data to make informed decisions. Discrete data is used to track quantities and counts, while continuous data provides precision for detailed analysis. For example, a company might track the number of units sold (discrete) and the average revenue per sale (continuous) to assess overall performance.
9.8 What are some examples of statistical analysis software that incorporate both continuous and discrete data inputs?
Most businesses use a range of statistical analysis software to surface business insights, incorporating both continuous and discrete data inputs. Some common types include:
- SPSS
- SAS
- R
- Python (with libraries like Pandas and NumPy)
- Excel
9.9 How does the discrete vs. continuous nature of money impact budgeting?
When creating a budget, you typically deal with discrete amounts. You allocate a fixed number of dollars to various categories. However, when tracking expenses, you might encounter transactions that involve continuous-like precision (e.g., gas prices calculated to the tenth of a cent per gallon).
9.10 What role does precision play in calculating compound interest, and how does it relate to the continuous nature of money?
The continuous-like nature of interest rates and the precision with which interest is calculated can have a significant impact on the final balance when calculating compound interest. The more precise the calculations, the more accurate the final result.
10. Discover the Best Financial Analysis Tools for Your Needs
Understanding your data is critical to maximizing its values and the insights gleaned from it. To get the most out of your data, you need to have the right tools. Head over to money-central.com for more information, along with tools and expert advice to manage your personal finances effectively. Whether you’re looking for resources on data preparation, digital analytics tools, data visualization platforms, or data catalog software, money-central.com provides comprehensive, easy-to-understand information.
Take control of your financial future today. Visit money-central.com to explore articles, tools, and resources designed to help you achieve your financial goals. Improve your financial health with the right insights and expert guidance now available at your fingertips.
Address: 44 West Fourth Street, New York, NY 10012, United States. Phone: +1 (212) 998-0000. Website: money-central.com.